本文转自: http://www.moonshile.com/post/juan-ji-shen-jing-wang-luo-quan-mian-jie-xi 感谢 Moonshile,写的很好,让本渣很容易懂。
最近仔细学习了一下卷积神经网络(CNN,Convolutional Neural Network),发现各处资料都不是很全面,经过艰苦努力终于弄清楚了。为了以后备查,以及传播知识,决定记录下来。本文将极力避免废话,重点聚焦在推导过程上,为打算从零开始的孩纸说清楚“为什么”。
另外,因本人才疏学浅(是真的才疏学浅,不是谦虚),肯定会有很多谬误,欢迎大家指出!
卷积神经网络(CNN)概述
- 由来:神经元网络的直接升级版
- 相关:Yann LeCun和他的LeNet
- 影响:在图像、语音领域不断突破,复兴了神经元网络并进入“深度学习”时代
卷积神经网络沿用了普通的神经元网络即多层感知器的结构,是一个前馈网络。以应用于图像领域的CNN为例,大体结构如图1。
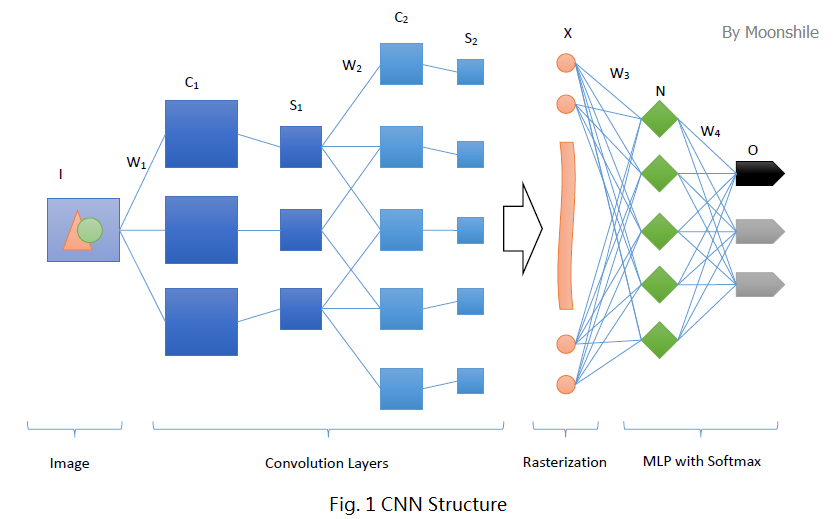
很明显,这个典型的结构分为四个大层次
- 输入图像I。为了减小复杂度,一般使用灰度图像。当然,也可以使用RGB彩色图像,此时输入图像有三张,分别为RGB分量。输入图像一般需要归一化,如果使用sigmoid激活函数,则归一化到[0, 1],如果使用tanh激活函数,则归一化到[-1, 1]。
- 多个卷积(C)-下采样(S)层。将上一层的输出与本层权重W做卷积得到各个C层,然后下采样得到各个S层。怎么做以及为什么,下面会具体分析。这些层的输出称为Feature Map。
- 光栅化(X)。是为了与传统的多层感知器全连接。即将上一层的所有Feature Map的每个像素依次展开,排成一列。
- 传统的多层感知器(N&O)。最后的分类器一般使用Softmax,如果是二分类,当然也可以使用LR。
接下来,就开始深入探索这个结构吧!
从多层感知器(MLP)说起
卷积神经网络来源于普通的神经元网络。要了解个中渊源,就要先了解神经元网络的机制以及缺点。典型的神经元网络就是多层感知器。
摘要:本节主要内容为多层感知器(MLP,Multi-Layer Perceptron)的原理、权重更新公式的推导。熟悉这一部分的童鞋可以直接跳过了~但是,一定一定要注意,本节难度比较大,所以不熟悉的童鞋一定一定要认真看看!如果对推导过程没兴趣,可直接在本节最后看结论。
感知器
感知器(Perceptron)是建立模型
$f(x) = act(\theta^Tx + b)$
其中激活函数 act 可以使用{sign, sigmoid, tanh}之一。
- 激活函数使用符号函数 sign ,可求解损失函数最小化问题,通过梯度下降确定参数
- 激活函数使用 sigmoid (或者 tanh ),则分类器事实上成为Logistic Regression(个人理解,请指正),可通过梯度上升极大化似然函数,或者梯度下降极小化损失函数,来确定参数
- 如果需要多分类,则事实上成为Softmax Regression
- 如要需要分离超平面恰好位于正例和负例的正中央,则成为支持向量机(SVM)。
感知器比较简单,资料也比较多,就不再详述。
多层感知器
感知器存在的问题是,对线性可分数据工作良好,如果设定迭代次数上限,则也能一定程度上处理近似线性可分数据。但是对于非线性可分的数据,比如最简单的异或问题,感知器就无能为力了。这时候就需要引入多层感知器这个大杀器。
多层感知器的思路是,尽管原始数据是非线性可分的,但是可以通过某种方法将其映射到一个线性可分的高维空间中,从而使用线性分类器完成分类。图1中,从X到O这几层,正展示了多层感知器的一个典型结构,即输入层-隐层-输出层。
输入层-隐层
是一个全连接的网络,即每个输入节点都连接到所有的隐层节点上。更详细地说,可以把输入层视为一个向量 (x) ,而隐层节点 (j) 有一个权值向量 (\theta_j) 以及偏置 (b_j) ,激活函数使用 sigmoid 或 tanh ,那么这个隐层节点的输出应该是
$f_j(x) = act(\theta_j^Tx + b_j)$
也就是每个隐层节点都相当于一个感知器。每个隐层节点产生一个输出,那么隐层所有节点的输出就成为一个向量,即
$f(x) = act({\Theta}x + b)$
若输入层有 (m) 个节点,隐层有 (n) 个节点,那么 (\Theta = [\theta^T]) 为 (n×m) 的矩阵,(x) 为长为 (m) 的向量,(b) 为长为 (n) 的向量,激活函数作用在向量的每个分量上, (f(x)) 返回一个向量。
隐层-输出层
可以视为级联在隐层上的一个感知器。若为二分类,则常用Logistic Regression;若为多分类,则常用Softmax Regression。
Back Propagation
搞清楚了模型的结构,接下来就需要通过某种方法来估计参数了。对于一般的问题,可以通过求解损失函数极小化问题来进行参数估计。但是对于多层感知器中的隐层,因为无法直接得到其输出值,当然不能够直接使用到其损失了。这时,就需要将损失从顶层反向传播(Back Propagate)到隐层,来完成参数估计的目标。
首先,约定标量为普通小写字母,向量为加粗小写字母,矩阵为加粗大写字母;再约定以下记号:
- 输入样本为 (\mathbf x),其标签为 (\mathbf t)
- 对某个层 (Q) ,其输出为 (\mathbf o_Q) ,其第 (j) 个节点的输出为 (o_Q^{(j)}) ,其每个节点的输入均为上一层 (P) 的输出 (\mathbf o_P) ;层 (Q) 的权重为矩阵 (\mathbf \Theta_Q) ,连接层 (P) 的第 (i) 个节点与层 (Q) 的第 (j) 个节点的权重为 (\theta_Q^{(ji)})
- 对输出层 (Y) ,设其输出为 (\mathbf o_Y), 其第 (y) 个节点的输出为 (o_Y^{(y)})
现在可以定义损失函数
$ \left \lbrace \begin {aligned} E & = \frac {1} {2} \sum_{y \in Y}(t^{(y)} - o_Y^{(y)})^2\ o_Q^{(j)} & = \phi(n_Q^{(j)})\ n_Q^{(j)} & = \sum_{i \in P} \theta_Q^{(ji)} o_P^{(i)} + b_Q^{(j)} \end {aligned} \right. $
其中, (\phi) 为激活函数。我们依旧通过极小化损失函数的方法,尝试进行推导。则
$ \left \lbrace \begin {aligned} \frac {\partial E} {\partial \theta_Q^{(ji)}} & = \frac {\partial E} {\partial o_Q^{(j)}} \frac {\partial o_Q^{(j)}} {\partial n_Q^{(j)}} \frac {\partial n_Q^{(j)}} {\partial \theta_Q^{(ji)}}\ \frac {\partial E} {\partial b_Q^{(j)}} & = \frac {\partial E} {\partial o_Q^{(j)}} \frac {\partial o_Q^{(j)}} {\partial n_Q^{(j)}} \frac {\partial n_Q^{(j)}} {\partial b_Q^{(j)}} \end{aligned}\right. $
上边两个式子的等号右边部有三个导数比较容易确定
$ \left \lbrace \begin {aligned} \frac {\partial o_Q^{(j)}} {\partial n_Q^{(j)}} & = \phi’(n_Q^{(j)})\ \frac {\partial n_Q^{(j)}} {\partial \theta_Q^{(ji)}} & = o_P^{(i)}\ \frac {\partial n_Q^{(j)}} {\partial b_Q^{(j)}} & = 1 \end {aligned} \right. $
然后再看剩下的比较复杂的一个偏导数。考虑层 (Q) 的下一层 (R) ,其节点 (k) 的输入为层 (Q) 中每个节点的输出,也就是为 (o_Q^{(j)}) 的函数,考虑逆函数,可视 (o_Q^{(j)}) 为 (o_R^{(k)}) 的函数,也为 (n_R^{(k)}) 的函数。则对每个隐层
$ \begin {aligned} \frac {\partial E} {\partial o_Q^{(j)}} & = \frac {\partial E(n_R^{(1)}, n_R^{(2)}, …, n_R^{(k)}, …, n_R^{(K)})} {\partial o_Q^{(j)}}\ & = \sum_{k \in R} \frac {\partial E} {\partial n_R^{(k)}} \frac {\partial n_R^{(k)}} {\partial o_Q^{(j)}}\ & = \sum_{k \in R} \frac {\partial E} {\partial o_R^{(k)}} \frac {\partial o_R^{(k)}} {\partial n_R^{(k)}} \frac {\partial n_R^{(k)}} {\partial o_Q^{(j)}}\ & = \sum_{k \in R} \frac {\partial E} {\partial o_R^{(k)}} \frac {\partial o_R^{(k)}} {\partial n_R^{(k)}} \theta_R^{(kj)} \end {aligned} $
令 (\delta_Q^{(j)} = \frac {\partial E} {\partial o_Q^{(j)}} \frac {\partial o_Q^{(j)}} {\partial n_Q^{(j)}})
则对每个隐层
$ \frac {\partial E} {\partial o_Q^{(j)}} = \sum_{k \in R} \frac {\partial E} {\partial o_R^{(k)}} \frac {\partial o_R^{(k)}} {\partial n_R^{(k)}} \theta_R^{(kj)} = \sum_{k \in R} \delta_R^{(k)} \theta_R^{(kj)} $
考虑到输出层,有
$ \frac {\partial E} {\partial o_Q^{(j)}} = \left \lbrace \begin {aligned} \sum_{k \in R} \delta_R^{(k)} \theta_R^{(kj)}, & \qquad k\ has\ input\ node\ j\ o_Y^{(j)} - t^{(j)}, & \qquad j\ is\ an\ output\ node,\ i.e.\ Q = Y \end {aligned} \right . $
故有
$ \delta_Q^{(j)} = \frac {\partial E} {\partial o_Q^{(j)}} \frac {\partial o_Q^{(j)}} {\partial n_Q^{(j)}} = \frac {\partial E} {\partial o_Q^{(j)}} \phi’(n_Q^{(j)}) = \left \lbrace \begin {aligned} (\sum_{k \in R} \delta_R^{(k)} \theta_R^{(kj)}) \phi’(n_Q^{(j)}), & \qquad k\ has\ input\ node\ j\ (o_Y^{(j)} - t^{(j)}) \phi’(n_Y^{(j)}), & \qquad j\ is\ an\ output\ node,\ i.e.\ Q = Y \end {aligned} \right. $
综合以上各式,有梯度结果
$ \begin {aligned} \frac {\partial E} {\partial \theta_Q^{(ji)}} & = \frac {\partial E} {\partial o_Q^{(j)}} \frac {\partial o_Q^{(j)}} {\partial n_Q^{(j)}} \frac {\partial n_Q^{(j)}} {\partial \theta_Q^{(ji)}} = \delta_Q^{(j)} o_P^{(i)}\ \frac {\partial E} {\partial b_Q^{(j)}} & = \frac {\partial E} {\partial o_Q^{(j)}} \frac {\partial o_Q^{(j)}} {\partial n_Q^{(j)}} \frac {\partial n_Q^{(j)}} {\partial b_Q^{(j)}} = \delta_Q^{(j)} \end {aligned} $
本来到这里应该就结束了,不过同正向的时候一样,为了计算方便,我们依然希望能够以矩阵或者向量的方式来表达。结论在这里:
假设有层 (P, Q, R) ,分别有 (l, m, n) 个节点,依序前者输出全连接到后者作为输入。层 (Q) 有权重矩阵 ([\mathbf \Theta_Q]{m×l}) ,偏置向量 ([\mathbf b_Q]{m×1}) ,层 (R) 有权重矩阵 ([\mathbf \Theta_R]{n×m}) ,偏置向量 ([\mathbf b_R]{n×1}) 。那么
$ \begin {aligned} \frac {\partial E} {\partial \mathbf \Theta_Q} & = \mathbf δ_Q \mathbf o_P^T\ \frac {\partial E} {\partial \mathbf b_Q} & = \mathbf δ_Q\ \mathbf δ_Q & = \left \lbrace \begin {aligned} (\mathbf \Theta_R^T \mathbf δ_R) \circ \phi’(\mathbf n_Q), & \qquad Q\ is\ a\ hidden\ layer\ (\mathbf o_Y - \mathbf t) \circ \phi’(\mathbf n_Y), & \qquad Q = Y\ is\ the\ output\ layer \end {aligned} \right. \end {aligned} $
其中,运算 (w = u \circ v) 表示 (w_i = u_i v_i) 。函数作用在向量或者矩阵上,表示作用在其每个分量上。
最后,补充几个常用的激活函数的导数结果,推导很简单,从略。
$ \begin {aligned} \phi’(x) & = sigmoid’(x) = sigmoid(x)(1 - sigmoid(x)) = \mathbf o_Q(1 - \mathbf o_Q)\ \phi’(x) & = tanh’(x) = 1 - tanh^2(x) = 1 - \mathbf o_Q^2\ \phi’(x) & = softmax’(x) = softmax(x) - softmax^2(x) = \mathbf o_Q - \mathbf o_Q^2 \end{aligned} $
存在的问题
多层感知器存在的最大的问题就是,它是一个全连接的网络,因此在输入比较大的时候,权值会特别多。比如一个有1000个节点的隐层,连接到一个1000×1000的图像上,那么就需要 10^9 个权值参数(外加1000个偏置参数)!这个问题,一方面限制了每层能够容纳的最大神经元数目,另一方面也限制了多层感知器的层数即深度。
多层感知器的另一个问题是梯度发散。 (这个问题的具体原因还没有完全弄清楚,求指教!) 一般情况下,我们需要把输入归一化,而每个神经元的输出在激活函数的作用下也是归一化的;另外,有效的参数其绝对值也一般是小于1的;这样,在BP过程中,多个小于1的数连乘,得到的会是更小的值。也就是说,在深度增加的情况下,从后传播到前边的残差会越来越小,甚至对更新权值起不到帮助,从而失去训练效果,使得前边层的参数趋于随机化(补充一下,其实随机参数也是能一定程度上捕捉到图像边缘的)。
感谢shwley提供的帮助~
因为这些问题,神经元网络在很长一段时间内都被冷落了。
从MLP到CNN
卷积神经网络的名字怪吓人,实际理解起来也挺吓人的。哈哈,其实只要看明白了多层感知器的推导过程,理解卷积神经网络就差不多可以信手拈来了。
摘要:首先解释卷积神经网络为什么会“长”成现在这般模样。然后详细推导了卷积神经网络的预测过程和参数估计方法。
CNN的前世今生
既然多层感知器存在问题,那么卷积神经网络的出现,就是为了解决它的问题。卷积神经网络的核心出发点有三个。
- 局部感受野。形象地说,就是模仿你的眼睛,想想看,你在看东西的时候,目光是聚焦在一个相对很小的局部的吧?严格一些说,普通的多层感知器中,隐层节点会全连接到一个图像的每个像素点上,而在卷积神经网络中,每个隐层节点只连接到图像某个足够小局部的像素点上,从而大大减少需要训练的权值参数。举个栗子,依旧是1000×1000的图像,使用10×10的感受野,那么每个神经元只需要100个权值参数;不幸的是,由于需要将输入图像扫描一遍,共需要991×991个神经元!参数数目减少了一个数量级,不过还是太多。
- 权值共享。形象地说,就如同你的某个神经中枢中的神经细胞,它们的结构、功能是相同的,甚至是可以互相替代的。也就是,在卷积神经网中,同一个卷积核内,所有的神经元的权值是相同的,从而大大减少需要训练的参数。继续上一个栗子,虽然需要991×991个神经元,但是它们的权值是共享的呀,所以还是只需要100个权值参数,以及1个偏置参数。从MLP的 10^9 到这里的100,就是这么狠!作为补充,在CNN中的每个隐藏,一般会有多个卷积核。
- 池化。形象地说,你先随便看向远方,然后闭上眼睛,你仍然记得看到了些什么,但是你能完全回忆起你刚刚看到的每一个细节吗?同样,在卷积神经网络中,没有必要一定就要对原图像做处理,而是可以使用某种“压缩”方法,这就是池化,也就是每次将原图像卷积后,都通过一个下采样的过程,来减小图像的规模。以最大池化(Max Pooling)为例,1000×1000的图像经过10×10的卷积核卷积后,得到的是991×991的特征图,然后使用2×2的池化规模,即每4个点组成的小方块中,取最大的一个作为输出,最终得到的是496×496大小的特征图。
现在来看,需要训练参数过多的问题已经完美解决。
而梯度发散的问题,因为还不清楚具体缘由,依然留待讨论。关于梯度发散,因为多个神经元共享权值,因此它们也会对同一个权值进行修正,积少成多,积少成多,积少成多,从而一定程度上解决梯度发散的问题!
下面我们来揭开卷积神经网络中“卷积”一词的神秘面纱。
CNN的预测过程
回到开头的图1,卷积神经网络的预测过程主要有四种操作:卷积、下采样、光栅化、多层感知器预测。
卷积
先抛开卷积这个概念不管。为简便起见,考虑一个大小为5×5的图像,和一个3×3的卷积核。这里的卷积核共有9个参数,就记为 (\Theta = [\theta_{ij}]_{3×3}) 吧。这种情况下,卷积核实际上有9个神经元,他们的输出又组成一个3×3的矩阵,称为特征图。第一个神经元连接到图像的第一个3×3的局部,第二个神经元则连接到第二个局部(注意,有重叠!就跟你的目光扫视时也是连续扫视一样)。具体如图2所示。
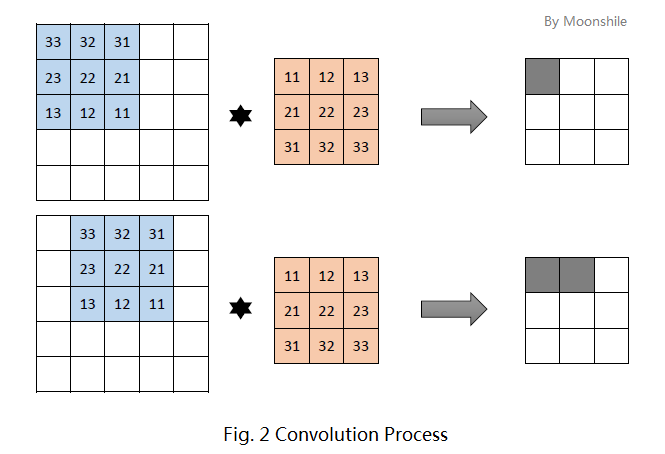
图2的上方是第一个神经元的输出,下方是第二个神经元的输出。每个神经元的运算依旧是
$f(x) = act(\sum_{i, j}^n \theta_{(n - i)(n - j)} x_{ij} + b)$
需要注意的是,平时我们在运算时,习惯使用 (\theta_{ij}x_{ij}) 这种写法,但事实上,我们这里使用的是 (\theta_{(n - i)(n - j)}x_{ij}) ,原因马上揭晓。
现在我们回忆一下离散卷积运算。假设有二维离散函数 (f(x, y), g(x, y)) , 那么它们的卷积定义为
$f(m, n)*g(m, n) = \sum_u^\infty \sum_v^\infty {f(u, v)g(m - u, n - v)}$
现在发现了吧!上面例子中的9个神经元均完成输出后,实际上等价于图像和卷积核的卷积操作!这就是“卷积神经网络”名称的由来,也是为什么在神经元运算时使用 (\theta_{(n - i)(n - j)}x_{ij}) 。
如果你足够细心,就会发现其实上述例子中的运算并不完全符合二维卷积的定义。实际上,我们需要用到的卷积操作有两种模式:
- valid模式,用 (*_v) 表示。即上边例子中的运算。在这种模式下,卷积只发生在被卷积的函数的定义域“内部”。一个 (m×n) 的矩阵被一个 (p×q) 的矩阵卷积( (m \ge p, n \ge q) ),得到的是一个 ((m - p + 1)×(n - q + 1)) 的矩阵。
- full模式,用 (*_f) 表示。这种模式才是上边二维卷积的定义。一个 (m×n) 的矩阵被一个 (p×q) 的矩阵卷积,得到的是一个 ((m + p - 1)×(n + q - 1)) 的矩阵。
现在总结一下卷积过程。如果卷积层 (c) 中的一个“神经中枢” (j) 连接到特征图 (\mathbf X_1, \mathbf X_2, …, \mathbf X_i) ,且这个卷积核的权重矩阵为 (\mathbf \Theta_j) ,那么这个神经中枢的输出为
$\mathbf O_j = \phi (\sum_i \mathbf X_i *_v \mathbf \Theta_j + b_j)$
下采样
下采样,即池化,目的是减小特征图,池化规模一般为2×2。常用的池化方法有:
- 最大池化(Max Pooling)。取4个点的最大值。这是最常用的池化方法。
- 均值池化(Mean Pooling)。取4个点的均值。
- 高斯池化。借鉴高斯模糊的方法。不常用。具体过程不是很清楚。。。
- 可训练池化。训练函数 (f) ,接受4个点为输入,出入1个点。不常用。
由于特征图的变长不一定是2的倍数,所以在边缘处理上也有两种方案:
- 忽略边缘。即将多出来的边缘直接省去。
- 保留边缘。即将特征图的变长用0填充为2的倍数,然后再池化。一般使用这种方式。
对神经中枢 (j) 的输出 (O_j) ,使用池化函数 downsample ,池化后的结果为
$\mathbf S_j = downsample(\mathbf O_j)$
光栅化
图像经过池化-下采样后,得到的是一系列的特征图,而多层感知器接受的输入是一个向量。因此需要将这些特征图中的像素依次取出,排列成一个向量。具体说,对特征图 (\mathbf X_1, \mathbf X_2, …, \mathbf X_j) ,光栅化后得到的向量
$\mathbf o_k = [x_{111}, x_{112}, …, x_{11n}, x_{121}, x_{122}, …, x_{12n}, …, x_{1mn}, …, x_{2mn}, …, x_{jmn}]^T$
多层感知器预测
将光栅化后的向量连接到多层感知器即可。
CNN的参数估计
卷积神经网络的参数估计依旧使用Back Propagation的方法,不过需要针对卷积神经网络的特点进行一些修改。我们从高层到底层,逐层进行分析。
多层感知器层
使用多层感知器的参数估计方法,得到其最低的一个隐层 (S) 的残差向量 (\mathbf δ_s) 。现在需要将这个残差传播到光栅化层 (R) ,光栅化的时候并没有对向量的值做修改,因此其激活函数为恒等函数,其导数为单位向量。
$\mathbf δ_R =(\mathbf \Theta_S^T \mathbf δ_S) \circ \phi’(\mathbf n_R) = \mathbf \Theta_S^T \mathbf δ_S$
光栅化层
从上一层传过来的残差为
$\mathbf δ_R = [\delta_{111}, \delta_{112}, …, \delta_{11n}, \delta_{121}, \delta_{122}, …, \delta_{12n}, …, \delta_{1mn}, …, \delta_{2mn}, …, \delta_{jmn}]^T$
重新整理成为一系列的矩阵即可,若上一层 (Q) 有 (q) 个池化核,则传播到池化层的残差
$\Delta_Q = {\mathbf \Delta_1, \mathbf \Delta_2, …, \mathbf \Delta_q}$
池化层
对应池化过程中常用的两种池化方案,这里反传残差的时候也有两种上采样方案:
- 最大池化:将1个点的残差直接拷贝到4个点上。
- 均值池化:将1个点的残差平均到4个点上。
即传播到卷积层的残差
$\mathbf \Delta_p = upsample(\mathbf \Delta_q)$
卷积层
卷积层有参数,所以卷积层的反传过程有两个任务,一是更新权值,另一是反传残差。先看更新权值,即梯度的推导。
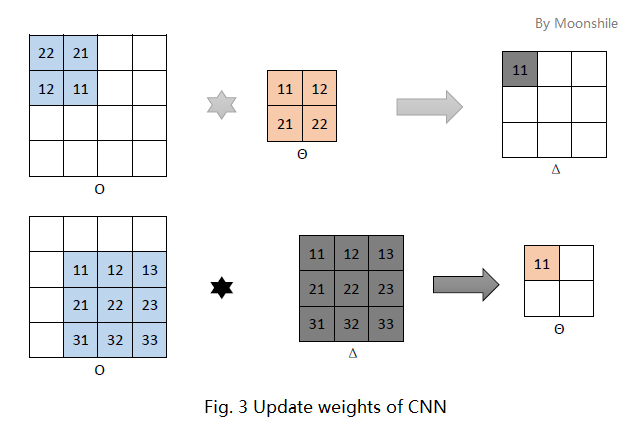
如图三上方,先考虑卷积层的某个“神经中枢”中的第一个神经元。根据多层感知器的梯度公式
$\frac {\partial E} {\partial \theta_{ji}} = \delta_j o_i$
那么在图三上方的例子中,有
$ \frac {\partial E} {\partial \theta_{11}} = \delta_{11} o_{22} \qquad \frac {\partial E} {\partial \theta_{12}} = \delta_{11} o_{21} \qquad \frac {\partial E} {\partial \theta_{21}} = \delta_{11} o_{12} \qquad \frac {\partial E} {\partial \theta_{22}} = \delta_{11} o_{11} $
考虑到其他的神经元,每次更新的都是这四个权值,因此实际上等价于一次更新这些偏导数的和。如果仅考虑对 (\theta_{11}) 的偏导数,不难发现如图3下方所示,其值应该来自于淡蓝色和灰色区域。是不是似曾相识?是的,又是卷积!但是又有两处重要的不同:
- 在计算对 (\theta_{11}) 的偏导数时,淡蓝色区域和灰色区域的对应位置做运算,但是在卷积运算中,这些位置应该是旋转过来的!
- (\theta_{11}) 在 (\Theta) 矩阵的左上角,而淡蓝色区域在右下角,同样是旋转过的!
因此,对卷积层 (P) 中的某个“神经中枢” (p), 权值(以及偏置,不再具体推导)更新公式应该是
$ \begin {aligned} \frac {\partial E} {\partial \mathbf \Theta_p} & = rot180((\sum_{q’} \mathbf O_{q’}) *v rot180(\mathbf \Delta_p))\ \frac {\partial E} {\partial b_p} & = \sum{u, v} (\delta_p)_{uv} \end {aligned} $
其中,(rot180) 是将一个矩阵旋转180度; (O_{q’}) 是连接到该“神经中枢”前的池化层的输出;对偏置的梯度即 (\Delta_p) 所有元素之和。
下面讨论残差反传的问题。
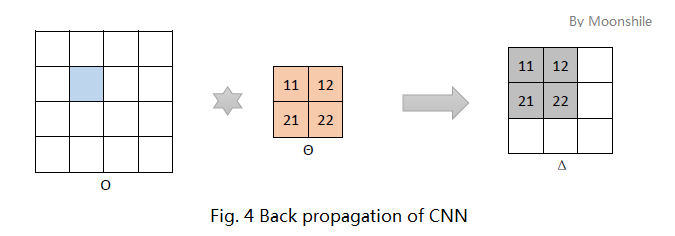
如图4,考虑淡蓝色像素点影响到的神经元,在这个例子中,受影响的神经元有4个,他们分别以某个权值与淡蓝色像素运算后影响到对应位置的输出。再结合多层感知器的残差传播公式,不难发现这里又是一个卷积过程!同样需要注意的是,正如图4中的数字标号,这里的卷积是旋转过的;另外,这里用的卷积模式是full。
如果前边的池化层 (Q’) 的某个特征图 (q’) 连接到这个卷积层 (P) 中的某“神经中枢”集合 (C) ,那么传播到 (q’) 的残差为
$\mathbf \Delta_{q’} = (\sum_{p \in C} \mathbf \Delta_p *f rot180(\mathbf \Theta_p)) \circ \phi’(\mathbf O{q’})$
最后一公里:Softmax
前边我有意忽略了对Softmax的讨论,在这里补上。因为Softmax的资料已经非常多了,所以这里不再详细讨论。具体可以参考这篇文章。
需要补充说明的是,不难发现,Softmax的梯度公式与多层感知器的BP过程是兼容的;另外,实现Softmax的时候,如果需要分为 (k) 个类,同样也可以设置 (k) 个输出节点,这相当于隐含了一个类别名称为“其他”的类。
CNN的实现
我建立了一个Github的repo,目前内容还是空的,近期会逐渐上传。
思路
以层为单位,分别实现卷积层、池化层、光栅化层、MLP隐层、Softmax层这五个层的类。其中每个类都有output和backpropagate这两个方法。
另外,还需要一系列的辅助方法,包括:conv2d(二维离散卷积,valid和full模式),downsample(池化中需要的下采样,两种边界模式),upsample(池化中的上采样),以及dsigmoid和dtanh等。
其他
还需要考虑的是可扩展性和性能优化,这些以后再谈~
自己想的神经网络
接下来的部分就是我自己想的了。
我想做一个复杂的网络,我认为现在的网络一旦固定了每一层的点就不会变化,这样做不出有思维的东西,于是我想做个可以改变每一层的点的位置,虽然没有什么依据,但是无聊看着还可以。
我们可以把一个神经网络看成一个图,于是我们的图在计算机的存放可以是矩阵,一个n阶矩阵。那么我们可以转矩阵为行列式。
用图可以矩阵来放在计算机,我们知道,行列式的变化,不会变化值,我们可以从图中找出行列式。
我们需要一定的初始化参数,于是我们使用大数,参数a,我们计算一个值a
for b=0.5;b<N;b++{ a=a*(1+b); b=b/2;}对所有行列式换
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
我们定义点
A=权值只有权值大于A的才可以B=交换 两列C=把一列`*n`加的一列D=交换 两行F=把一行`*n`加的一行H=交换点顺序N=赋值点权值- 使用 点 改图
- 使用 图 训练

本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可。 欢迎转载、使用、重新发布,但务必保留文章署名 林德熙 (包含链接: https://blog.lindexi.com ),不得用于商业目的,基于本文修改后的作品务必以相同的许可发布。如有任何疑问,请与我 联系。